
Sorting Algorithms in JavaScript
Commonly used sorting algorithms in Javascript
In this post, I want to cover commonly used sorting algorithms using JavaScript. These algorithms reduce the complexity of a problem. Sorting algorithms are used to organize an array of elements into a specific order.
For example:
[5, 2, 9] ----- SORT -----> [2, 5, 9]
We’ll have a look at the following commonly used algorithms:
- Bubble sort
- Insertion sort
- Merge sort
- Quick sort
Then onwards we’ll look at the efficiency of these algorithms.
Bubble sort
It follows a recursion technique. We start with comparing two elements of an array, and swap them if required. We continue till the end of the array. We repeat this process until the array is sorted.

Let’s have a look how we can implement this,
function bubbleSort(arr){
for(let i = 0; i < arr.length; i++){
for(let j = 0; j < arr.length - i - 1; j++){
//Value comparison using ascending order
if(arr[j + 1] < arr[j]){
//Swapping
[arr[j + 1],arr[j]] = [arr[j],arr[j + 1]]
}
}
};
return arr;
};
console.log(bubbleSort([5,3,8,4,6]));
// Output: [ 3, 4, 5, 6, 8 ]
Bubble sort has the following performance cases:
- Worst-case time complexity: O( n^2 )
- Average case time complexity: O(n)
- Best case complexity: O(1)
Insertion sort
It also uses the recursion technique where one portion of the array is sorted and the other is unsorted. So we have to compare elements from the unsorted portions and insert them in sorted order.
- We assume the first element is sorted, so we start from the second element.
- When comparing the first and second elements, whichever is lowest, get inserted at the first position.
- Next, we do the same process for all elements of the array.

Let’s look how we can implement it,
function insertionSort(arr){
//Start from the second element.
for(let i = 1; i < arr.length;i++){
//Go through the elements behind it.
for(let j = i - 1; j > -1; j--){
//value comparison using ascending order.
if(arr[j + 1] < arr[j]){
//swap
[arr[j+1],arr[j]] = [arr[j],arr[j + 1]];
}
}
};
return arr;
}
console.log(insertionSort([23, 1, 10, 5, 2]));
// Output: [ 1, 2, 5, 10, 23 ]
Insertion sort has the following performance cases:
- Worst-case time complexity: O( n^2 )
- Average case time complexity: O(n)
- Space complexity: O(1)
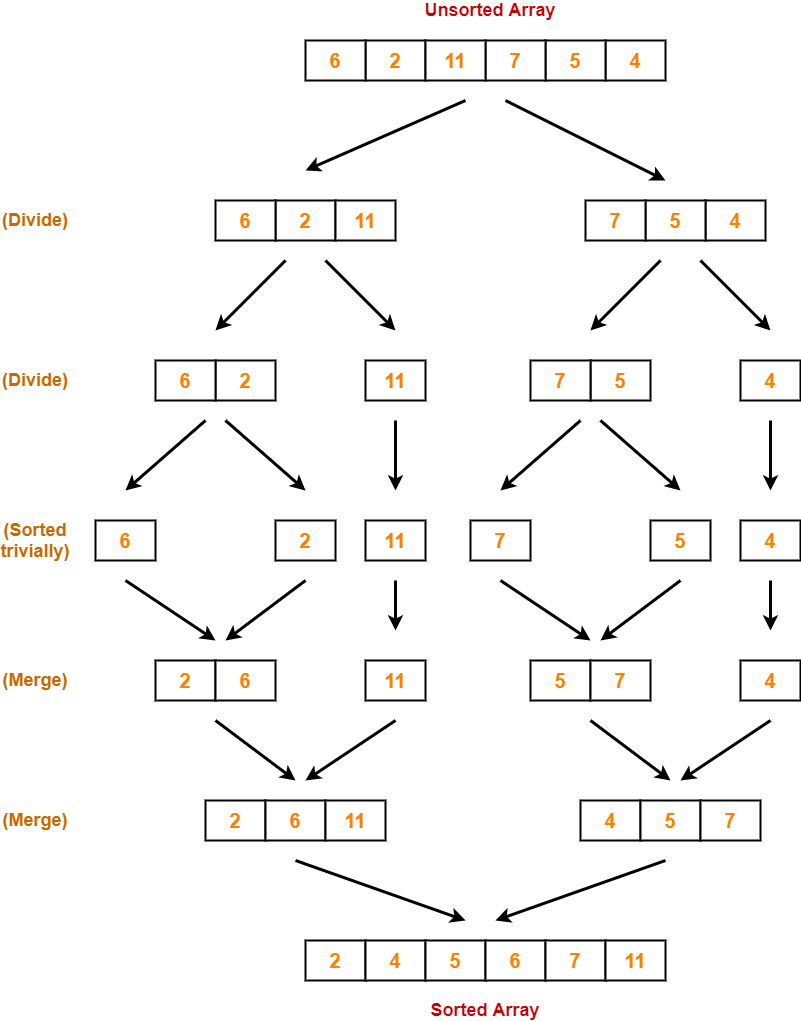
Merge sort
Merge sort uses a divide and conquer algorithm. Unlike other sorting algorithms. Merge sort doesn’t care if the input array is sorted or not. It always performs the same operations regardless.
- We divide the original array into smaller arrays until each small array has one position/element left.
- These smaller arrays are then merged into a final sorted one.
function merge(left, right) {
let arr = []
// Break out of loop if any one of the array gets empty
while (left.length && right.length) {
// Pick the smaller among the smallest element of left and right sub arrays
if (left[0] < right[0]) {
arr.push(left.shift())
} else {
arr.push(right.shift())
}
}
// Concatenating the leftover elements
// (in case we didn't go through the entire left or right array)
return [ ...arr, ...left, ...right ]
}
function mergeSort(array) {
const half = array.length / 2
// Base case or terminating case
if(array.length < 2){
return array
}
const left = array.splice(0, half)
return merge(mergeSort(left),mergeSort(array))
}
In the snippet above, first, we take two sorted subarrays and merge them into a single sorted array. One thing to understand, if there are an odd number of elements, the left one gets a smaller number of elements. We divide until we are left with single-element arrays.
Merge sort has the following performance cases:
- Worst-case time complexity: O(n log (n))
- Average case time complexity: O(n log (n))
- Space complexity: O(n)
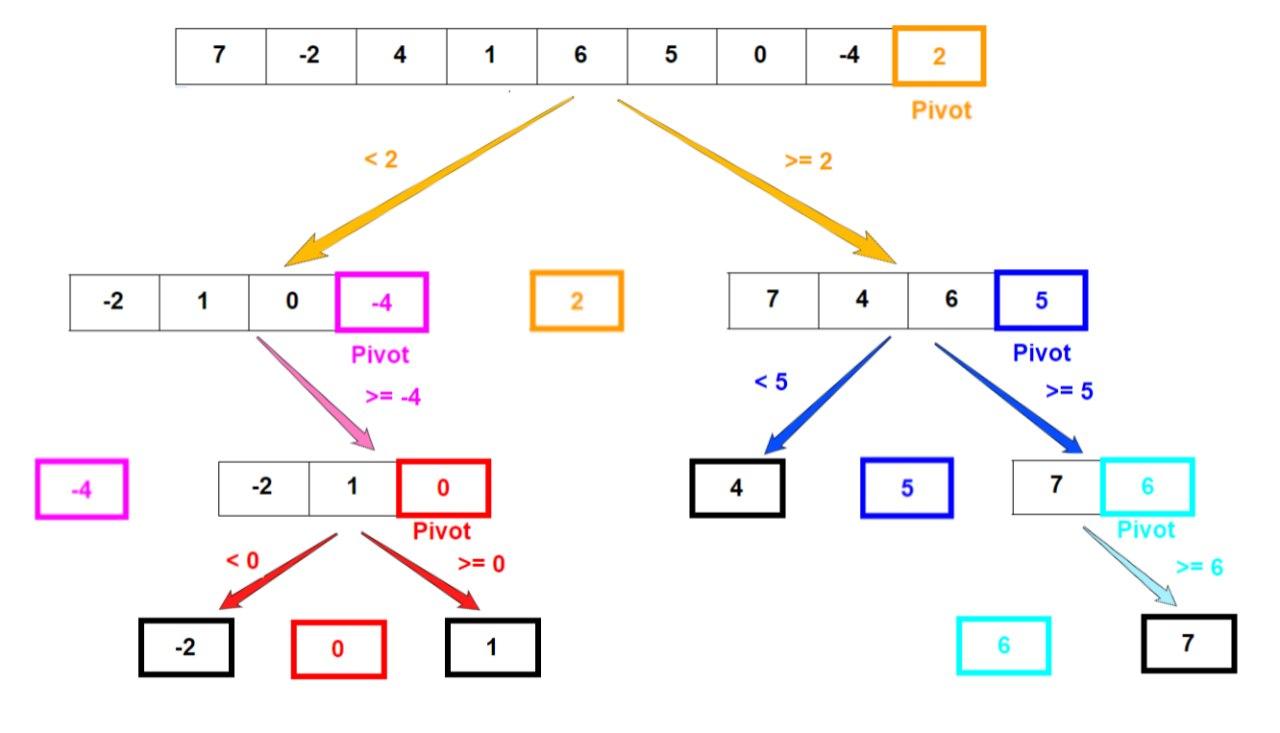
Quick sort
This is one of the most used sorting algorithms. Similar to merge sort, we use the divide and conquer approach for this. It is considered the fastest method to sort. It can be implemented recursively or iteratively.
- Select the first element of the array, we call it pivot. It can be the first or last item of the array.
- Then we rearrange elements of an array in such a way elements to the left of the pivot are smaller than the pivot and righter elements are greater than it.
- Repeat this process individually for each side of the pivot.
Let’s look at the implementation in JavaScript
function partition(items, left, right) {
//rem that left and right are pointers.
let pivot = items[Math.floor((right + left) / 2)],
i = left, //left pointer
j = right; //right pointer
while (i <= j) {
//increment left pointer if the value is less than the pivot
while (items[i] < pivot) {
i++;
}
//decrement right pointer if the value is more than the pivot
while (items[j] > pivot) {
j--;
}
//else we swap.
if (i <= j) {
[items[i], items[j]] = [items[j], items[i]];
i++;
j--;
}
}
//return the left pointer
return i;
}
function quickSort(items, left, right) {
let index;
if (items.length > 1) {
index = partition(items, left, right); //get the left pointer returned
if (left < index - 1) {
//more elements on the left side
quickSort(items, left, index - 1);
}
if (index < right) {
//more elements on the right side
quickSort(items, index, right);
}
}
return items; //return the sorted array
}
let items = [5, 3, 7, 6, 2, 9];
console.log(quickSort(items, 0, items.length - 1));
// Output: [ 2, 3, 5, 6, 7, 9 ]
Quick sort has following performance cases:
- Worst-case time complexity: O( n^2 )
- Average/Best case time complexity: O(n log (n))
- Space complexity: O(log(n))
This algorithm could be used for sorting large arrays. Quick sort is often compared with Merge sort, both have average time complexity of O(n log (n)), this could be ignored if we take the last element as pivot. Merge Sort is quicker when dealing with linked lists.
Conclusion
We’ve covered commonly used algorithms for sorting. With this understanding, we can figure out an appropriate sorting algorithm to use depending on the dataset, time complexity, and space available.

